馬可夫矩陣
一個 \(n\times n\) 的實數方陣 \(M\) 如果滿足
- \(M\) 的每一項都大於等於 \(0\),且
- \(M\) 的每一列的列和均等於 \(1\),
則被稱為 馬可夫矩陣(Markov matrix)。
馬可夫矩陣又被稱為 轉移矩陣(transition matrix),原因是它的 \(i,j\)-項可以被視為是從狀態 \(i\) 轉換到狀態 \(j\) 的機率。以下圖來說
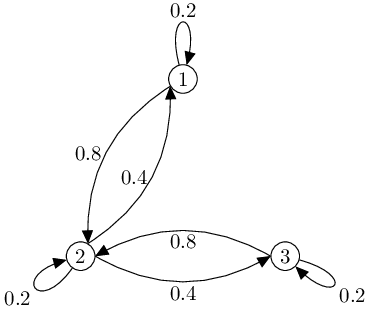
想像有一個人在圖上旅行,每一步都會在附近的點依照邊上分配的機率來隨機選一點前進。比如說從 \(1\) 號點出發,則他在下一步有 \(20\%\) 的機率留在 \(1\) 號點、\(80\%\) 的機率移動到 \(2\) 號點,而只走一步的情況下不可能從 \(1\) 號點移動到 \(3\) 號點。這樣的 隨機漫步(random walk) 的過程可以被記錄在成一個矩陣
也就是一個馬可夫矩陣。
因此馬可夫矩陣和隨機漫步有直接的對應,而馬可夫矩陣定義中的兩個條件可以翻譯成隨機漫步表現在賦權有向圖(weighted digraph)的條件,也就是
- 每條有向邊的權重都大於 \(0\),若沒有邊則視為權重等於 \(0\),且
- 每一點連出去的所有有向邊,其權重總和為 \(1\)。
這樣兩種面向(矩陣和圖)的關連性,正是代數圖論關心的重點之一。
由於整個過程有許多隨機的成份,我們可以用一個向量 \(\bx\trans = (p_1,\ldots,p_n)\) 來表示隨機漫步當下停留在各點的機率,因此我們要求每一個 \(p_i \geq 0\) 且 \(\sum_{i=1}^n p_i = 1\);這樣的一個向量是一個機率分布,我們稱之為 態(state),它記錄了當下的所有資訊。比如說 \(\be_1\trans = (1,0,\ldots,0)\) 意思是 \(100\%\) 停留在 \(1\) 號點上。考慮離散的時間 \(t = 0, 1, \ldots\),如果 \(\bx_t\trans\) 是時間 \(t\) 當下的態,則我們有
這樣的關係。因此如果一個態 \(\pi\trans\) 滿足
則我們稱 \(\pi\trans\) 為 穩定態(stationary state)。它是一個隨機漫步裡的特殊狀況。
穩定態一定會存在嗎?如果專注在有向圖上會很難說明它一定存在,然而矩陣提供另外一種面向,告訴我們任何的馬可夫矩陣都有穩定態。考慮全 \(1\) 向量 \(\bone\trans = (1,\ldots,1)\trans\)。則我們知道 \(M\bone = \bone\)。注意這裡向量乘在右邊,所以它跟前述的態不太一樣。然而這樣的等式告訴我們 \((M - I)\bone = \bzero\) 且 \(M - I\) 是一個奇異(singular)矩陣。這表示 \(M - I\) 的左側一定也有一個非零向量 \(\pi\trans\) 使得 \(\pi\trans(M - I) = \bzero\trans\),也就是 \(\pi\trans M = \pi\trans\)。如果恰巧 \(\pi\) 的各項都大於等於 \(0\) 且總和為 \(s\),則 \(\frac{1}{s}\pi\trans\) 為一穩定態,而未來我們會用佩弗定理(Perron–Frobenius theorem)來說明這樣的穩定態一定存在。
想想以下問題:
- 穩定態唯一嗎?
- 找出 \(M = \begin{bmatrix} 0 & 1 \\ 1 & 0 \end{bmatrix}\) 的所有穩定態。
- 找出 \(M = \begin{bmatrix} 0.5 & 0.2 & 0.3 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \\ \end{bmatrix}\) 的所有穩定態。
- 隨機漫步久了以後一定會趨向穩定態嗎?
- 令 \(M = \begin{bmatrix} 0 & 1 \\ 1 & 0 \end{bmatrix}\) 且初始態為 \(\bx_0 = (1,0)\),描述 \(\bx_t\) 長期的變化。
- 令 \(M = \begin{bmatrix} 0.2 & 0.8 \\ 0.8 & 0.2 \end{bmatrix}\) 且初始態為 \(\bx_0 = (1,0)\),描述 \(\bx_t\) 長期的變化。
- 考慮集合 \(S\) 為所有 \(n\) 維態的集合。利用固定點定理(Brouwer fixed-point theorem)來說明穩定態一定存在。