我相信你一定聽過，內積就是投影，這個講法基本上沒有問題，但是，你是否曾想過為何內積的計算方法是這樣，仔細想想不覺得很神奇嗎？為何簡單的逐項相乘再相加，會產生出投影的效果，雖然內積基本上貫徹了整個線性代數，但我相信不少人並不了解為何內積是這樣計算的。

單位向量所代表的意義

我們先給一個單位向量 \(\begin{bmatrix} \frac{1}{2} \\ \frac{\sqrt{3}}{2} \end{bmatrix}\)，然後我們把它畫出來，如下

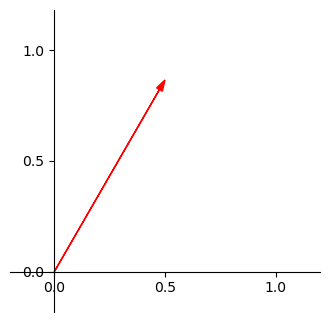
現在，我們用一種比較不一樣的角度來理解這個向量中的分量 \(\frac{1}{2}\) 與 \(\frac{\sqrt{3}}{2}\) 分別所代表的意義，我們把它拆成標準基底的線性組合，如下

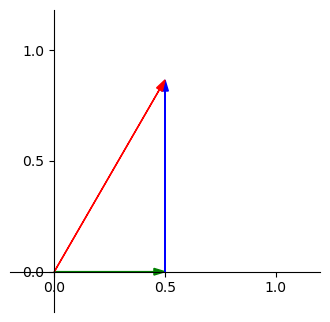
圖中綠色的向量是 \(\begin{bmatrix} \frac{1}{2} \\ 0 \end{bmatrix}\)，藍色的向量是 \(\begin{bmatrix} 0 \\ \frac{\sqrt{3}}{2} \end{bmatrix}\)，也可以寫成 \(\frac{1}{2} \begin{bmatrix} 1 \\ 0 \end{bmatrix}\) 跟 \(\frac{\sqrt{3}}{2} \begin{bmatrix} 0 \\ 1 \end{bmatrix}\)，現在，我們先關注紅色跟綠色之間的關聯性，我們先將紅色向量與 \(\begin{bmatrix} 1 \\ 0 \end{bmatrix}\) 畫出來，如下
（這邊的藍色向量與上面的藍色向量無關）

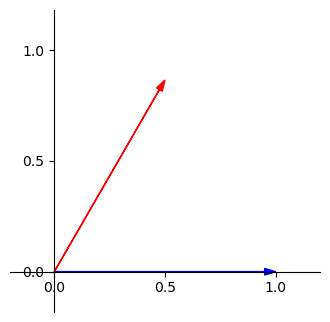
然後我們把紅色向量投影在 \(\begin{bmatrix} 1 \\ 0 \end{bmatrix}\) 上面，如下

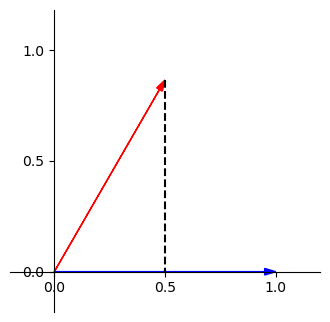
這時就會發現其對應的投影剛好是 \(\frac{1}{2} \begin{bmatrix} 1 \\ 0 \end{bmatrix}\) ，也就是紅色向量在 \(x\) 軸上的分量，畫出來就是下面這樣

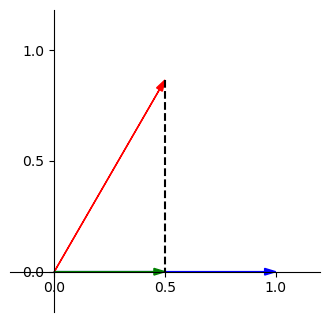
看到這裡，一定會覺得我講了一堆廢話，但我想表達的重點是「單位向量的分量就是投影長」。

注意看下面這張圖

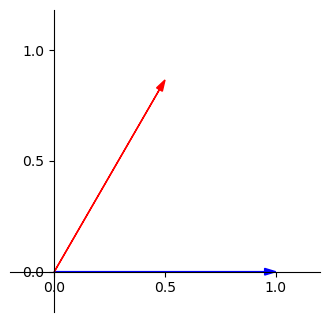
我們上面在關注的是紅色投影到藍色上的結果，但是在這裡紅色和藍色向量都是單位向量，因此我們知道紅色投影在藍色上，跟藍色投影在紅色上的投影長是相等的，因此可以把投影的角色翻轉，如下

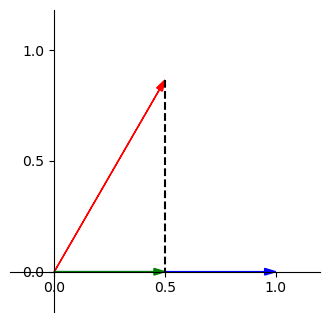\(\implies\)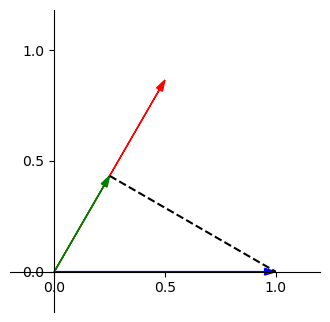

因此，我們現在對單位向量的分量又產生了另一種理解方式，也就是「單位向量的分量就是其對應的基底元素在自己身上的投影長」，有了這個理解，基本上就離理解內積不遠了。

所以對於在 \(y\) 軸上的分量，我們也可以有一樣的理解，如下

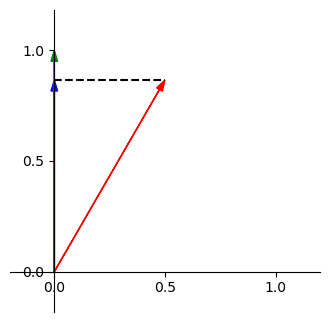\(\implies\)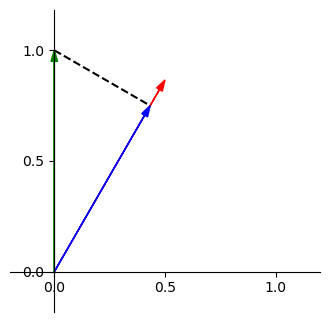

單位向量的內積

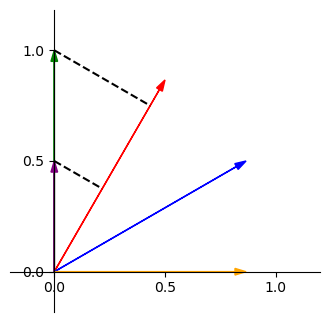
現在我們給定兩單位向量 \(\begin{bmatrix} \frac{1}{2} \\ \frac{\sqrt{3}}{2} \end{bmatrix}\) 與 \(\begin{bmatrix} \frac{\sqrt{3}}{2} \\ \frac{1}{2} \end{bmatrix}\)，然後我們把它畫出來，如下

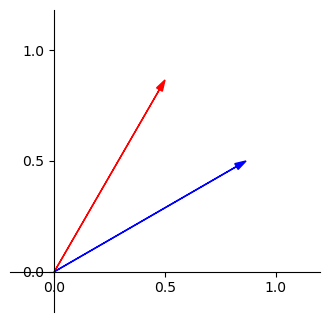
我們知道這兩個向量內積的值，就是藍色向量投影在紅色向量上的投影長（因為紅色是單位向量），我們先將藍色向量拆成分量的線性組合，如下

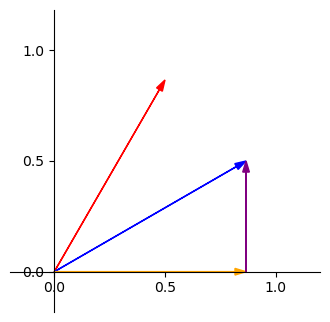
要計算藍色在紅色上的投影長，我們可以分別計算橘色和紫色在紅色上的投影長後再加總，如下

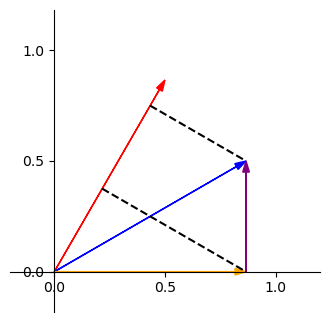
我們先試著計算黃色向量的投影長。

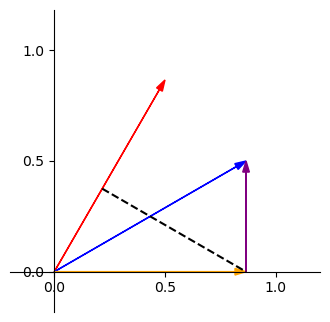
至於要怎麼計算，就需要用到上面對單位向量的特殊理解法，我們先把單位向量與其之投影畫出來。

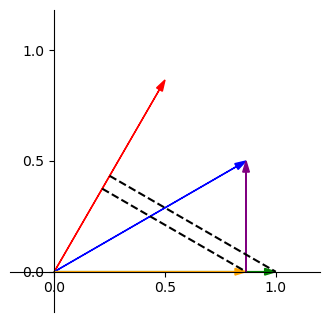
圖中的綠色向量就是 \(x\) 方向上的單位向量，根據我們上面對單位向量的理解，它在紅色向量上的投影長就是紅色向量的 \(x\) 分量的大小，也就是 \(\frac{1}{2}\)，但我們實際要求的是黃色在紅色上的投影長，那這個值與 \(\frac{1}{2}\) 差多少呢？看圖應該不難知道，其實只差一個倍數，而這個倍數就是黃色的長度，也就是藍色向量的 \(x\) 分量的值 \(\frac{\sqrt{3}}{2}\)，因此我們得知黃色在紅色上的投影長是 \(\frac{1}{2} \times \frac{\sqrt{3}}{2}\)。

到這裡不知道有沒有發現，其實 \(\frac{1}{2}\) 與 \(\frac{\sqrt{3}}{2}\) 就剛好對應到紅色與藍色向量的第一個分量，相乘的動作也就是內積在做的逐項相乘。

接著我們來看紫色向量的部分，我們先將其平移至原點，如下

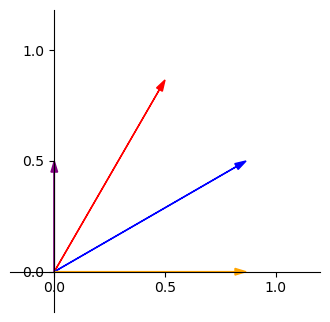
然後我們一樣把投影的線和單位向量都畫上去。

這邊也一樣，我們知道綠色在紅色上的投影長是紅色的 \(y\) 分量，也就是 \(\frac{\sqrt{3}}{2}\)，而紫色在紅色上的投影長則與之相差了 \(\frac{1}{2}\) 倍，也就是藍色向量的 \(y\) 分量的值，因此紫色向量的投影長就是 \(\frac{\sqrt{3}}{2} \times \frac{1}{2}\) 也就是 \(y\) 分量的值相乘。

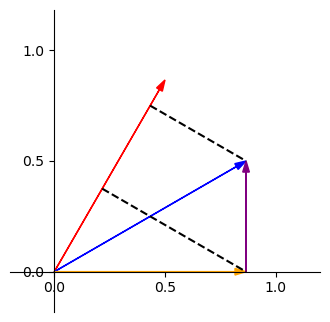
最後我們根據這張圖，我們知道藍色向量在紅色向量上的投影長就是黃色和紫色在紅色上的投影長相加，也就是 \(\frac{1}{2} \times \frac{\sqrt{3}}{2} + \frac{\sqrt{3}}{2} \times \frac{1}{2}\)，與內積的計算方式相同，但我們卻是用幾何觀點來完成的。

一般向量的內積

上面我們解釋了單位向量的內積，而對於一般情況下的內積，其實也非常相似。

給定兩向量 \(5 \begin{bmatrix} \frac{1}{2} \\ \frac{\sqrt{3}}{2} \end{bmatrix}\) 與 \(2 \begin{bmatrix} \frac{\sqrt{3}}{2} \\ \frac{1}{2} \end{bmatrix}\)，如下

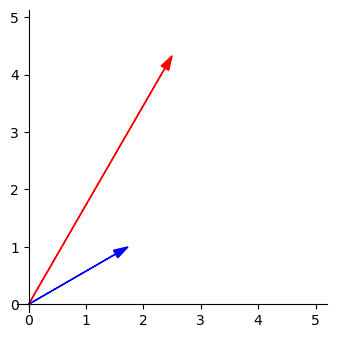
我們剛剛已經學會如何計算 \(\begin{bmatrix} \frac{1}{2} \\ \frac{\sqrt{3}}{2} \end{bmatrix}\) 與 \(\begin{bmatrix} \frac{\sqrt{3}}{2} \\ \frac{1}{2} \end{bmatrix}\) 的內積了，其實這兩個問題是非常類似的，如果上面都了解的話，應該不難理解，其實這兩個問題只差了 \(5\) 跟 \(2\) 這兩個倍數，寫成數學式就是

\[\langle 5 \begin{bmatrix} \frac{1}{2} \\ \frac{\sqrt{3}}{2} \end{bmatrix}, 2 \begin{bmatrix} \frac{\sqrt{3}}{2} \\ \frac{1}{2} \end{bmatrix} \rangle = 5 \times 2 \times \langle \begin{bmatrix} \frac{1}{2} \\ \frac{\sqrt{3}}{2} \end{bmatrix}, \begin{bmatrix} \frac{\sqrt{3}}{2} \\ \frac{1}{2} \end{bmatrix} \rangle\]

幾何上感覺也是挺直觀的事情，可以想像成先將向量單位化後內積，最後在把長度乘回去，因此在遇到一般情況下的向量，先將兩者都單位化，我們就可以套用上面的方式去理解了。